Collection of numeric algorithms. More...
Functions | |
| __int128 | xgcd (__int128 p_a, __int128 p_b, __int128 &p_s, __int128 &p_t) |
| Extended Euclidean algorithm. | |
| bool | isint128 (std::string p_str) |
| Is the string a 128 bit integer. | |
| bool | isint128 (const mpz_t p_x) |
| Is the multiple precision integer a 128 bit integer. | |
| int32_t | rand (uint32_t *seed) |
| ISO C rand_r() for 32 bit. | |
Detailed Description
Collection of numeric algorithms.
Function Documentation
◆ isint128() [1/2]
| bool algo::isint128 | ( | const mpz_t | p_x | ) |
Is the multiple precision integer a 128 bit integer.
- Parameters
-
[in] p_x mpz_t to check
- Returns
- boolean ... for an assert.
◆ isint128() [2/2]
| bool algo::isint128 | ( | std::string | p_str | ) |
Is the string a 128 bit integer.
- Parameters
-
[in] p_str String to check
- Returns
- boolean ... for an assert.
◆ rand()
| int32_t algo::rand | ( | uint32_t * | seed | ) |
ISO C rand_r() for 32 bit.
- Parameters
-
[in,out] seed ... random generator seed.
- Returns
- pseudo random value between 0 and
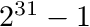
◆ xgcd()
| __int128 algo::xgcd | ( | __int128 | p_a, |
| __int128 | p_b, | ||
| __int128 & | p_s, | ||
| __int128 & | p_t | ||
| ) |
Extended Euclidean algorithm.
Calculates the gcd of both input integers and additionally calculates a pair of Bézout coefficients s and t such that gcd(a,b) = s*a + t*b. Returns 0 if both p_a and p_b are 0.
- Parameters
-
[in] p_a first input number [in] p_b second input number [out] p_s a Bézout coefficient of p_a [out] p_t a Bézout coefficient of p_b
- Postcondition
- gcd(a,b) = p_s*p_a + p_t*p_b
- Returns
- gcd of p_a and p_b